Relation of Radians and Angular Velocity to AC Circuits
Radians and angular velocity are terms that are commonly used in AC theory and AC measurement. Most of the electric energy used commercially is generated as Alternating Current (AC). The main reason Alternating Current is used is that alternating voltage may be easily raised or lowered in value. This is a tremendous advantage in electrical distribution systems, allowing AC power to be generated and distributed at a high voltage and reduced to a more practical voltage at the load. In today’s discussion we will look at the relation of radians and angular velocity to Alternating Current circuit. AC is produced when a conductor rotates through a magnetic field. This results in a waveform which is referred to as a sine wave.
Sine wave
The sine wave is an electrical waveform that is created when the amplitude or the amount of the signal is varied proportional to the sine of the angle through which the conductor is rotating at any given instant in time. It is a very common type of alternating current that is produced by either a rotating electrical machine, such as a generator, or by an electronic oscillator. As the conductor rotates around the circumference of a circle, it is traveling 360 degrees. These points of degrees can be illustrated on the waveform. For example, a full rotation or a full waveform is 360 degrees, half a rotation or half a waveform is a 180 degrees. The image below illustrates the formation of a sine wave as a conductor rotates through 360 degrees.
Radians
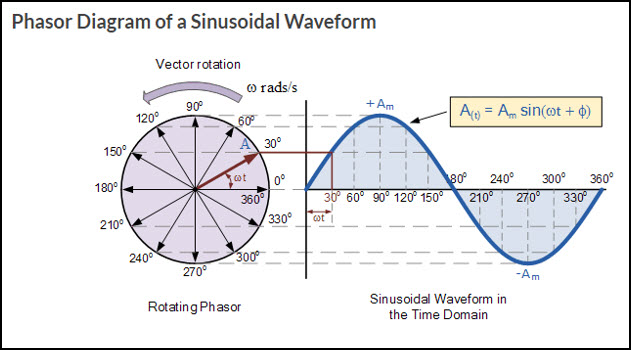
Earlier we looked at the formation of sine wave as the conductor rotates through 360 degrees. Now, we will learn to measure angles in radians. In AC circuits, angles are frequently measured in radian, rather than degrees. Radian is defined by an arc of a circle where the length of an arc is equal to the radius of the circle.The circumference of a circle equals 2πr where r is the radius. A complete circle will therefore have 2π radians, which is subtended by 360°. In other words, to calculate how many degrees are in a radian, you can state the number of radians in the circle as 2π radians, which is equal to the number of degrees in a circle (360 degrees). So the number of degrees in a radian can be found by dividing 360° by 2π.
Formula: 2πr = 360°, r = 360°/2π, 1 radian = 57.3°
Angular Velocity
Angular Velocity is another term that's related to Radian measure. It is the time rate of change in angular displacement. This is equal to the distance traveled by the conductor, which is measured in radians, divided by the period(T), time taken for one revolution. The term angular velocity can also be stated with a letter symbol ω, which is the lowercase Greek letter Omega. Therefore, Omega is equal to so many radians per second. If we look at just one waveform, then ω is equal to 2π radians over time in seconds i.e. (ω = 2π/T). The angle through which the conductors move in one second may be written as:
Angular velocity = ω = 2π/T (radians/second)
Another term we will discuss that relates to radian measure and angular velocity is frequency. Frequency (f) refers to the number of cycles or waveforms per second with unit of hertz or Hz. In formula, f = 1/T. If we combine the formulas of the last two terms, we arrive at angular velocity or Omega equal to 2πf.
Given: ω = 2π/T and f = 1/T, therefore T= 1/f, combined ω = 2π/ (1/f) = 2πf
The term omega ω is a term that you will encounter in a number of formulas as you study AC theory in electricity and electronics.
We hope this has been helpful to you as a technican or a student entering the field. If you have any questions about the Electronics or Electromechanical Technician programs you can reach one of our Program Consultants toll free at 1-888-553-5333 or by email at info@gbctechtraining.com.
Comments
HVAC
Submitted by tyrone loukas (not verified) on Wed, 05/15/2024 - 04:09
Understanding the relationship between radians and angular velocity in AC circuits is like finding the key to unlock the mysteries of electrical engineering. Grateful for this insightful connection that not only deepens our comprehension but also empowers us to navigate and innovate within the realm of alternating current systems.
HVAC
Submitted by tyrone loukas (not verified) on Thu, 08/08/2024 - 04:13
Thank you so much for clarifying the connection between radians, angular velocity, and AC circuits! Your explanation has really helped me understand how these concepts interact and their importance in electrical engineering. I appreciate the effort you put into making such complex ideas more accessible!
HVAC
Submitted by David Grace (not verified) on Thu, 12/12/2024 - 07:20
This is a fascinating article that sheds light on the intricate relationship between radians, angular velocity, and AC circuits. It's a great way to visualize and understand the underlying principles of alternating current. Thank you for sharing this insightful information!

Students from different countries are all very welcome in our programs. Our programs are based on a self-paced, self-study model that works very well for distance education students anywhere. And with the curriculum available on a USB with additional resources online, it is very simple for anyone, anywhere, to register and successfully complete the program. Even our technical and tutorial support can be easily accessed through online forums and email, regardless of your time zone.