How to Perform Loop or Mesh Analysis on a Linear DC Network Using Kirchhoff’s Voltage Law

Loop current analysis or mesh analysis is an analytical method to determine the current flowing at different points in a closed circuit. Kirchhoff’s voltage law and Ohm’s law are used to calculate the current flowing through each resistor and their corresponding voltage drops, when performing loop analysis in a circuit.

There are six general steps are required to perform a loop or mesh circuit analysis on a resistive DC network.

1. Identify and assign arbitrarily a direction to the loop currents in the circuit.
2. Mark the polarity of the elements in each loop in terms of our assumed current direction.
3. Create the Kirchhoff’s Voltage Law (KVL) equation for each loop in terms of the specified loop direction.
4. Use Ohm's law. to specify the unknown KVL voltages in each loop equation in terms of current and resistance.
5. Calculate the KVL voltage expressions for each loop in the circuit, use substitution and elimination to solve for the unknown loop currents.
6. Use the loop currents to calculate resistor current and voltage throughout the circuit.

 

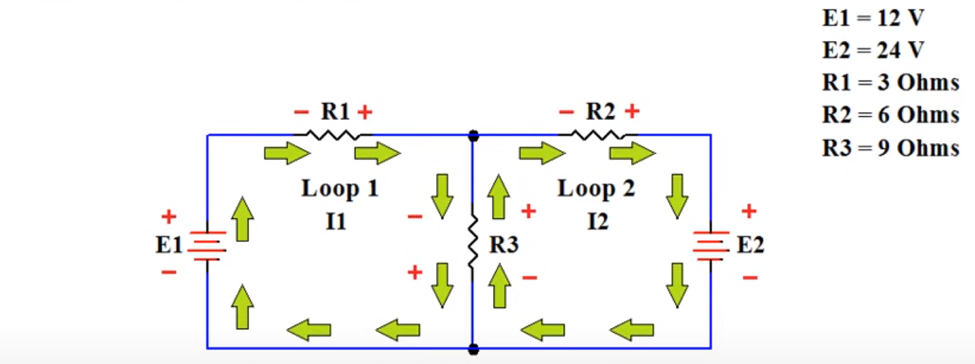
Identify and assign a direction to the loop currents 

To analyze the above circuit, we will begin by identifying and assigning a direction to the loop

currents in the circuit. The first loop current I₁ flows through resistor R₁, resistor R₃ and voltage source E₁. We have chosen arbitrarily a clockwise direction to represent the current flowing around Loop 1 in the circuit. The second loop current I₂ flows through resistor R₂, voltage source E₂, and resistor R₃. As with loop one, we have also assigned clockwise current for the second loop.

 Mark the polarity of the elements

 

Next, we will mark the polarity of the elements for each loop in terms of the assumed current direction that we have already assigned. Starting with loop 1, we will mark the known polarity of the voltage source E1. According to the electron flow, we know that current enter to the negative end of the element and exit through the positive end. We can assign polarity to the remaining element of the loop 1 according to that. For loop 2, first we will mark the known polarity of the voltage source E2 and then assign polarity of the remaining elements according to the electron flow.

 Create the KVL equation for each loop

 

In the third step of the process, we will be constructing Kirchhoff’s voltage law equation for each loop in the circuit. We will start from the upper left-hand corner of loop 1 and travel around the loop in a clockwise direction. When you travel from the negative end of an element to the positive end of an element, the voltage is considered positive and is added when constructing the KVL expression. On the other hand, if you travel from the positive end of an element to the negative end of an element, the voltage is subtracted in the KVL equation. Considering the voltage across the resistor R₁, we're moving from negative to positive. This means that this value is added or positive. For the voltage across resistor R₃, we are once again moving from negative to positive, so this voltage is added as well. We complete our walk around the loop by considering the voltage on E₁. This voltage also is added as we're moving from negative to positive. Kirchhoff's voltage law states that the algebraic sum of the voltages around any given loop must equal zero. We therefore set this new equation equal to zero for loop 1.

 

                                                         V_R1 + V_R3 + E₁ = 0

 

Now we will construct the KVL equation for loop 2 in same way. Starting in the upper left corner of loop 2, we once again move in a clockwise direction around the loop. For voltage across the resistor R₂, we're moving from negative to positive, so the value is added or considered to be positive. When we come to the E₂ voltage source, we're moving from positive to negative polarity, therefore, the value of E₂ is subtracted in the KVL equation. For voltage across the resistor R₃, we're moving from negative to positive, so the value is added, and the entire equation is set to equal zero for loop 2.

 

                                                          V_R2 – E₂ + V_R3 = 0

 

Use Ohm's law to specify the unknown KVL voltages

Next, we will be using Ohm's law to re-express the voltage drops in each of the loop equations. Beginning with loop 1, the R₁ voltage drop can be restated as the value of R₁ times current I₁. When expressing the voltage drop across R₃ in this manner, it's important to note that the current for R₃ is a combination of I₁ and I₂. As we have expressed the I₁ and I₂ currents as moving in opposite directions, the value of the voltage drop across R₃ for loop 1 will be the value of R₃ times the I₁ current less the I₂ current. For loop1,

                                                         R₁*I₁ + R₃*(I₁ – I₂) + E₁ = 0

 

When we deal with loop 2, this R₃ current value will be expressed as (I₂ – I₁). Now we will substitute the known resistance and sources values into the modified KVL equation of loop 1. Next, we will expand the equation and then collect like terms to state the equation with unknowns on one side and a known voltage on the other.

 

Here the values that have already given, E₁ = 12 V, E₂ = 24 V, R₁ = 3 Ohm, R₂ = 6 Ohm, R₃ = 9 Ohm. So, substituting these values in loop 1 equation we get,

 

                                                          3*I₁ + 9*(I₁ – I₂) + 12 = 0 

                                                   3I₁ + 9I₁ – 9I₂ + 12 = 0                   

                                                                   12I₁ – 9I₂ = -12  

 

We will repeat the process for loop 2 to obtain the Ohms law representation of the loop 2 KVL equation Notice that as we will be working with loop 2, the I₁ current will be subtracted from the I₂ reference current when we will be considering the voltage drop across R₃. Then we will substitute in our known values, expand the equation, collect like terms, and separate those terms with unknown quantities from those of constant value voltages. Now that we have 2 KVL equations with 2 unknowns, I₁ and I₂.  

 

                                                 R₂*I₂ – E₂ + R₃*(I₂ – I₁) = 0 

                                                    6*I₂ – 24 + 9*(I₂ – I₁) = 0 

                                                           6I₂ – 24 + 9I₂ – 9I₁ = 0

                                                                           -9I₁ + 15I₂ = 24

Calculate unknown currents using KVL voltage expressions for each loop in the circuit

 

Now we will solve these unknown values. To get the value of current I₁, we will eliminate the I₂ terms from these equations. To do this we will find the lowest common multiple for the I₂ coefficients. In this case will be 45. This is accomplished by multiplying the loop 1 equation by 5, and by multiplying the loop 2 equation by 3. Depending on the sign of the I₂ coefficients, we either add or subtract these two new equations from each other to eliminate the I₂ term and solve for I₁

 

                                                      60I₁ – 45I₂ = -60

                                                     -27I₁ + 45I₂ = 72

 

Since the coefficients for I₂ do not have the same sign, we will therefore add the equations and it will result in zero I₂. Once the I₂ term will be eliminated, we will proceed by solving for I₁.

 

                                                      60I₁ – 45I₂ = - 60

                                                    -27I₁ + 45I₂   = 72

                                                       33I₁ + 0I₂   = 12

                                                                         I₁  = 12/33

 I₁  = 0.363636 A

 I₁  = 363.636 mA

After obtaining the value of the I₁ loop current, we will use substitution to obtain the I₂ loop current. Using the loop 1 equation, we will substitute in the value for I₁ and proceeded to calculate the value of I₂. Using loop 1,

                                                      12(0.363636) – 9I₂ = -12

                                                               4.363632 – 9I₂ = -12

                                                                                         -9I₂ = -12 – 4.363632

                                                                                             I₂ = -16.363632/-9

                                                                                                                  I₂ = 1.81818 A

 

To confirm the validity of our calculation, we could also substitute the I₁ value into the loop 2 equation and we should end up at the exact same result. Using loop2,

 

                                                     -9(0.363636) +15I₂ = 24

                                                                           -3.2727 + 15I₂ = 24

                                                                                       15I₂ = 27.272724

                                                                                             I₂ = 27.272724/15

                                                                                             I₂ = 1.81818A

 

It is also important to note that instead of solving for I₁ by eliminating I₂ as we did at the start step 5, we could just as easily have solved for I₂ by eliminating I₁.

 

Having determined the value of I₁ and I₂, it is easy to calculate the value of I_R3, and move on to the final step of the process. Because the loop 2 and loop 1 currents flowing through resistor R₃ are flowing in opposite directions and the loop 2 current is larger, the net resulting current, I₃ will flow in the same direction as loop current I₂.

                                                                                           I₃ = I₂ – I₁

                                                                                           I₃ = 1.818 – 0.363636

                                                                                           I₃ = 1.454 A

Use the loop currents to calculate resistor current and voltage

 

With all three resistor currents known, it is a simple matter of applying Ohm's law to calculate the voltage drop across each resistor. The voltage drop across the resistor R₁ is,

 

                                                                                                             V_R1 = I₁ x R₁

                                                                                                                      = 0.363636 x 3

                                                                               = 1.091 volt

Resistor R₂ is dropping,

 

                                                                                             V_R2 = I₂ x R₂

                                                                                                                           = 1.81818 x 6

                                                                                = 10.909 volt

 

Finally, we calculate the voltage drop across resistor R₃,

 

      V_R3 = I₃ x R₃

                                                                                                                            = 1.454 x 9

                                                                                 = 13.086 volt

 

In this example, we tried to explain the steps of analyzing a circuit using loop current analysis or mesh analysis. Using loop analysis, we can easily calculate the voltage drop of different elements in the circuit and the amount of current flowing through them as well.

 

We hope that this has been helpful as a student or practicing Electronics technician. If you have any questions regarding the Electronics Technician program, feel free to get in touch with us at [email protected] or give us a call at 1-888-553-5333 to speak with a Program Consultant.